무엇이 통제입니까?

개시하다
안녕하세요.목공/계수 Advent Calendar 2021째 날.
오늘은 제어공학이라는 분야를 gif 애니메이션을 통해 소개합니다.
사실 현재 계수공학에서 학생들은 계수를 더 잘 알 수 있는 흥분된 블로그를 만들겠다는 포부를 가지고 있다.이 보도도 그 블로그에 공개될 것이다.또 계수공학을 소재로 한 게임도 공개할 예정이니 공학 박람회 트위터를 팔로우하고 후속 보도를 기다려주세요!
제어 공학
통제란 자신의 생각대로 대상을 조종하는 것이다.영어로 컨트롤하면 더 잘 알겠지?제어공학의 응용 범위는 매우 넓어서 공학의 많은 장소에서 사용된다.
물구나무 진자
물구나무 진자는 제어의 필수품으로 계수공과 실험에서도 사용된다.물구나무 진자의 상황 설정은 밑차에 시계추가 있어서 시계추를 물구나무 세우고 싶다는 것이다.물론 그대로 두면 시계추가 쓰러진다.

거기서 컨트롤할 차례야.피드백 제어를 사용하면 완전히 상반된 상태에서 유지할 수 있다.아래gif 그림은 거의 움직이지 않는 것처럼 보이지만, 이것은 제어하에 유지되어 있기 때문입니다.

피드백 제어
피드백 제어의 구조는 아래의 그림으로 표시한다.

컨트롤러의 목표는 컨트롤 대상의 상태를 목표 값과 일치시키는 것이다.따라서 컨트롤러는 먼저 센서로 제어 대상의 상태를 측정하여 목표 값과 $e(t)$의 차이를 계산한다.컨트롤러는 집행기를 통해 제어 대상에 영향을 미칠 수 있기 때문에 $e (t) $0 달러 차이를 내기 위해 집행기에 어떤 사령관을 보내는 것이 좋을지 계산합니다.
고전적 통제 이론
컨트롤러의 디자인에 대해 컨트롤 이론에서 가능한 한 빠르고 안정적으로 목적 상태를 달성하는 시스템을 목표로 하는 관점에서 출발하여 각양각색의 토론과 개량을 진행하였다.이번에는 드론을 통해 다양한 통제 방법을 시도해보자.무인기가 레드라인을 타는 것은 목표의 높이다.

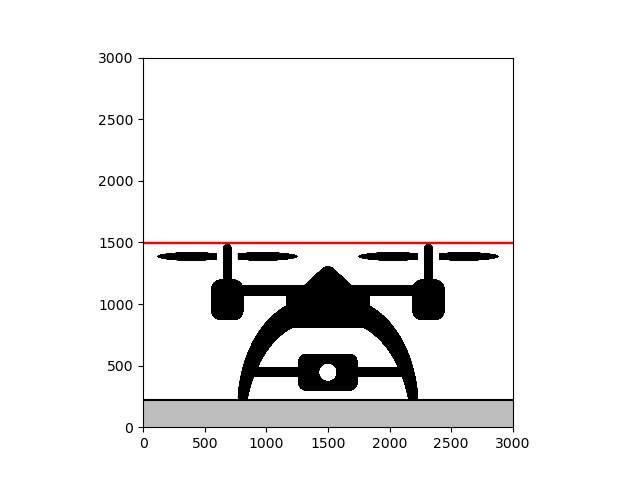
뱅뱅 컨트롤
가장 간단한 제어는 출력이 목표 값에 미달할 때 제어 입력을 제공하고 목표 값을 초과할 때 입력을 닫으며 ON/OFF 제어를 한다.ON/OFF 제어는 전문 용어에서 뱅뱅 제어(반 제어)라고 불린다.어감이 좀 재밌네.
레드라인 아래에서 프로펠러를 돌리고, 레드라인을 넘으면 스톱프로펠러 제어로 드론을 건너뛴다.

대체로 목표 높이 근처에서 제어할 수 있지만 아래 높이의 시간 도표에서 높이가 위아래로 이동하는 것을 볼 수 있다.

도표를 보면 진동폭이 줄지 않아 목표치 근처에서 계속 진동하는 것을 예상할 수 있다.이러면 안정적이라고 할 수 없잖아.
뱅뱅 제어는 효과적인 예로 에어컨을 들 수 있다.방 온도가 조금 오르락내리락해도 아무도 신경 안 쓰겠지.따라서 예를 들어 냉방 설정온도가 28℃일 경우 실온이 28℃ 이하일 때는 냉방을 멈추고, 실온이 28℃ 이상일 때는 냉방을 가동시키는 제어를 통해 실온을 약 28℃ 부근으로 유지할 수 있다.
P 제어
출력 및 목표 값의 차이 $e(t)$에 비례하는 제어 입력을 사용하는 제어를 P 제어라고 합니다.P는 축척의 첫 글자입니다.편차가 $e(t)$로 표시되면 $u(t)$입력을 제어하여 양비례 이득$K$\mathrm{P}
$$
u(t) = K_\mathrm{P}\cdot e(t)
$$
구문을 사용합니다.
뱅뱅 제어에서는 목표치에 근접하더라도 0% 또는 100%의 제어 입력만 입력할 수 있기 때문에 목표치 근처에서 진동이 지속되지만 P 제어는 미세하게 조정할 수 있기 때문에 상태가 일정치로 수렴될 수 있다.


확실히 상태는 끝났지만 그 수렴치는 목표에서 벗어난 값이다.목표 값에 가까울수록 제어 입력이 작아져 외부 간섭(중력)의 영향을 없앨 수 없기 때문이다.그럼에도 불구하고 안정적인 편차가 0에 가까워 이득을 더하기 위해 이번 시스템의 호응은 지나치게 진동하여 발산되었다.
PI 제어
안정적인 편차를 0으로 설정하기 위해서, 적분기 제어 (integral control) 를 가져옵니다.편차를 시간 포인트로 진행하여 제어 입력에 추가합니다.이렇게 되면 안정적인 편차를 없애는 제어 입력이 늘어나 목표치로 수렴될 전망이다.제어 입력은 다음과 같다.
$$
u(t) = K_\mathrm{P} e(t) + K_\mathrm{I}\int_0^t e(\tau) d\tau
$$
PI 컨트롤로 드론 건너뛰자.

이번에 중력의 영향을 잘 보상받아서 빨간 선을 탔어요.다만, 완전히 마무리하기 전에 이미 몇 차례 선을 넘었다.

PID 제어
응답 속도를 높이기 위해 마이크로프로세서 제어(differential control)를 넣습니다.축척, 적분기 조합의 3가지 제어를 PID 제어라고 하는데 제어 입력은 다음과 같이 공식적이다.
$$
u(t) = K_\mathrm{P} e(t) + K_\mathrm{I}\int_0^t e(\tau) d\tau + K_\mathrm{D}\frac{d e(t)}{d t}
$$
미분항을 포함하기 때문에 급격한 목표치의 변화와 외부 방해에 대해 신속하게 반응하고 제어 입력에 반영되기 때문에 목표치를 더욱 빨리 수렴할 수 있다.
PID 컨트롤로 드론 건너뛰자.우리는 그것이 매우 잘 수렴될 뿐만 아니라 수렴 속도도 매우 빠르다는 것을 분명히 볼 수 있다.

고도의 도표를 보세요.PI 제어는 목표를 크게 넘어섰지만 가져오기 마이크로미터를 통해 이것이 억제된 것임을 알 수 있다.

각양각색의 통제 이론
이번에는 PID 컨트롤, 컨트롤 이론에 대한 다양한 연구 방법을 소개했다.
현대 제어 이론
방금 전의 무인기 시스템은 PID 제어를 통해 고성능 제어를 진행하였다.PID 제어는 매우 실용적이어서 세계의 절반 이상의 시스템이 PID에 의해 제어된다고 한다.그러나 PID 제어에는 시스템이 대규모이고 복잡할 때 대응할 수 없는 문제가 존재한다.예를 들어 최초의 물구나무 진자의 예는 어떻습니까?물구나무 진자를 세우고 가운데에 놓으려면 어떻게 컨트롤해야 하나요?대답할 수 있는 건 현대적 통제야.
현대 통제 이론에서 우리의 목표는 통제 선형 체계의 관점에서 분석함으로써 본질적인 구조를 풀는 것이다.모두가 알다시피 시스템 구조의 아름다운 정리, 예를 들어 통제와 관측이 가능한 쌍배합성에 관한 것이다.
최적 제어
최적 제어는 어떤 지침값(평가 함수)을 최소화하는 제어이다.평가 함수는 제어의 목적에 따라 설정된다. 예를 들어 출력과 편차의 크기를 가중시키고 합친 값이나 목표 위치에서 멈출 때의 시간 등이다.사실 처음에 보여준 물구나무 진자의 예도 LQR이라는 최상의 제어를 사용하여 제어한 것이다.이런 방법이 평가 함수를 결정하면 컨트롤러가 설계할 수 있기 때문에 PID 제어의 매개 변수 조정 대신 평가 함수를 설계하면 목적에 맞는 컨트롤러를 설계하기 쉽다.
노봉 제어
실제 시스템과 수리 모델 사이에는 모델링 오차라고 불리는 오차가 존재한다.이 원인은 여러 가지가 있는데 만약에 간단한 수리모델로 복잡한 시스템과 비슷하거나 복잡한 수리모델을 사용하여 간소화한 수리모델, 모델의 매개 변수 추측(시스템 식별)의 오차 등이 주요 원인이다.이 모델링 오차로 실제 시스템의 성능이 악화되고 때로는 불안정해질 수도 있다.이런 상황에서'이 범위의 오차는 반드시 안정될 것이다'는 보증을 하는 것은 안정적인 통제이다.
참고 문헌
[1] 삼강준치, 등전정지,, 일관회사, 1999.
[2] MathWorks, PID 제어, https://jp.mathworks.com/discovery/pid-control.html.
[3] 2018년도 공박회 이론책인 에서
링크
이 페이지의 에뮬레이션github 공개