Juria를 사용하여 부드러운 곡선 SVG 내보내기

개요

Plots.jl로 출력된 도표(곡선)는 접선이어서 좀 끊깁니다.

BasicBSpline 패키지 출력을 사용하면 Bnozier 곡선과 비슷하게 나와서 좋아요!

본 문서에 사용된 패키지는 Juria의 REPL에서 다음 명령을 사용하여 설치할 수 있습니다.

]add Plots
add StaticArrays
add BasicBSpline
add https://github.com/hyrodium/BasicBSplineExporter.jl

Plots.jl 출력

Plots.소프트웨어 패키지를 사용하여 차트를 출력합니다.

using Plots

plot(sin,-8,8)  # 正弦波を-8から8までプロット
savefig("sin_Plots.svg")  # SVGで保存
savefig("sin_Plots.png")  # PNGで保存

SVG 이미지를 최대값 근처에서 확대합니다.


너 되게 멋있구나.[1]
커브가 폴리라인과 비슷하기 때문입니다.다음 이미지는 SVG 이미지를 확인하기 위해 Inkscape를 여는 곳입니다.

어떻게 해야만 매끄러운 도표를 얻을 수 있습니까?
SVG에서는 Bnozier 곡선에 대응하기 때문에 파일 형식으로는 가능할 것 같은데...
→BasicBSpline으로 포장하세요!

BasicBSplineExporter.jl 출력

using BasicBSpline
using BasicBSplineExporter
using StaticArrays

f(t) = SVector(t,sin(t)) # 正弦波のパラメータ表示
t0,t1 = -8,8             # 左端と右端

p = 3                                     # 多項式次数。SVGでは3次までのBézier曲線が使える。
k = KnotVector(t0:t1)+p*KnotVector(t0,t1) # ノット列
P = BSplineSpace{p}(k)                    # B-spline空間の定義

a = fittingcontrolpoints(f,(P,))  # B-spline曲線の制御点の計算
M = CustomBSplineManifold(a,(P,)) # B-spline曲線の定義
save_svg("sin_BasicBSpline.svg", M, xlims=(-10,10), ylims=(-2,2)) # B-spline曲線をSVGで保存
save_png("sin_BasicBSpline.png", M, xlims=(-10,10), ylims=(-2,2)) # B-spline曲線をPNGで保存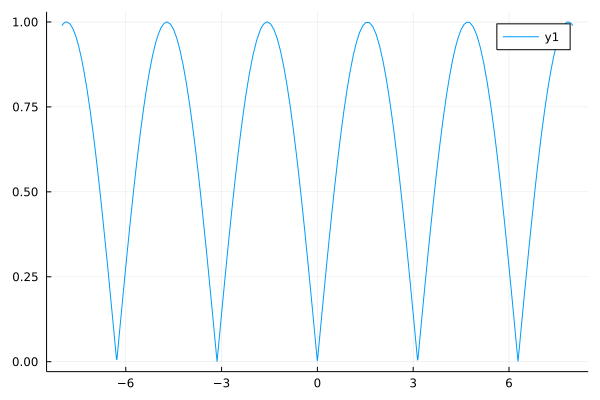![](https://storage.googleapis.com/zenn-user-upload/731678b5e5e8-20211229.png)

Inkscape로 확인하면 다음과 같이 Bnozier 곡선으로 매끄럽게 곡선이 표현되는 것을 알 수 있습니다.


위에서 정의한 B-spline 곡선은 노트의 위치에 연결되어 전체적으로 C^2 레벨의 매끄러움을 줍니다.각 구간은 다항식이기 때문에 곡선은 다항식을 구분하는 것으로 표시된다.

매끄럽지 않을 때(Plats.jl)

f(x)=||sin(x)|의 도표를 그려보세요.
Plots.jl에서 다음과 같이 그림을 출력할 수 있습니다.

plot(abs∘sin,-8,8)
savefig("abssin_Plots.svg")
savefig("abssin_Plots.png")

접선이 비슷하기 때문에 도함수의 불연속점이라도 특징을 잡는 도표로 볼 수 있다.
그러나 첨단을 확대해 보면 도표가 y축에 맞지 않아 특이점 근처에서 비뚤어져 보인다.

매끄럽지 않을 때(BasicBSpline.jl)

이전과 같이 다음 동작을 실행하면 도표를 출력할 수 있습니다.

f(t) = SVector(t,abs(sin(t)))
t0,t1 = -8,8
p = 3
k = KnotVector(range(t0,t1,length=50))+p*KnotVector(t0,t1)
P = BSplineSpace{p}(k)

a = fittingcontrolpoints(f,(P,))
M = CustomBSplineManifold(a,(P,))
save_svg("abssin_BasicBSpline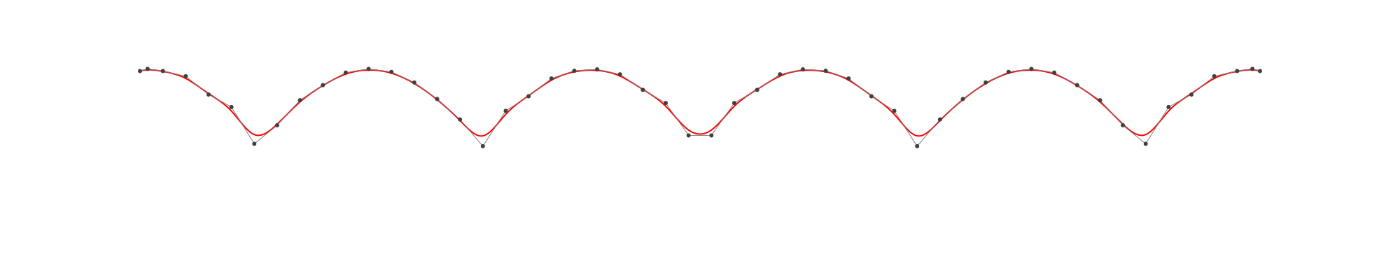![](https://storage.googleapis.com/zenn-user-upload/555b66bd3bac-20211229.png).svg", M, xlims=(-10,10), ylims=(-2,2))
save_png("abssin_BasicBSpline.png", M, xlims=(-10,10), ylims=(-2,2))

출력된 이미지↓

도함수 불연속점의 증폭↓

비록 not의 수량(다항식 분할수 구분)이 증가하더라도'매끄러운 연결'의 제약이 있기 때문에 근사 정밀도는 좋아지지 않는다.
B-spline에서는 not의 중복 감소 함수의 매끄러움[2]에 따라 in의 뿌리 부분에 여러 개의 not를 배치하면 된다.

k = KnotVector(range(t0,t1,length=12))+p*KnotVector(t0,t1)
k += p*KnotVector(-2π:π:2π)  # 滑らかさを減らしたい点でのノットを増やす
P = BSplineSpace{p}(k)

a = fittingcontrolpoints(f,(P,))
M = CustomBSplineManifold(a,(P,))
save_svg("abssin_BasicBSpline_modified.svg", M, xlims=(-10,10), ylims=(-2,2))
save_png("abssin_BasicBSpline_modified.png", M, xlims=(-10,10), ylims=(-2,2))

출력된 이미지↓

확대해도 예뻐요!↓

총결산

BasicBSpline 등의 포장을 사용하면 매끄러운 도표를 출력할 수 있어 편리합니다!

B-spline에서 not열의 중복에 따라 매끄러움을 바꿀 수 있어 편리합니다!

먼저 그리려면 Plates를 사용합니다.포장이 편리합니다!

각주
이번에는 GR 백엔드를 사용하여 검증을 진행하고 있습니다.다른 백엔드라면 바뀔 수도 있어요.↩︎
정확히 말하면 n점의 not가 중복되면 이 점에서 C^{p-n}급의 매끄러움에 도달할 수 있다.↩︎