#010 DS&A- 시간과 공간 분석
소개
너 말고는 할 말이 없어.👋,
현수막에 있는 이 사람이 누군지 알고 싶다면 알고리즘 개념의 발명자인 Khwarizmi다.
반드시 따라주십시오. 왜냐하면 저는 미래에 더욱 고급스러운 시리즈를 시작할 것입니다.
알고리즘
시간과 공간 분석
점근 분석 도론
컴퓨터 과학의 모든 문제를 해결하기 위해서 우리는 보통 프로그램을 작성하는데, 프로그램을 작성하기 전에 형식화된 설명, 즉 알고리즘으로 작성하는 것이 가장 좋다.
만약에 우리가 문제가 하나 있다고 가정하면P 우리는 프로그램을 써야 한다. 우리는 c로 그것을 써야 한다. 프로그램을 쓰려면 먼저 알고리즘을 써야 한다. 가설P에는 다른 해와 다른 해s1,s2,s3,s4....와 다른 해time가 많은데 그의 과학은 memory라고 한다.
알고리즘에 사용되는 기호는 다음과 같습니다.
점근 기호
Oh는

입력이 증가함에 따라 시간이 증가하면 최악의 경우 또는 상위 경계 Design and analysis of algorithm 를 충족합니다.
f(n) <= C*g(n) ; n >= n0 ; c>0 , n0 >= 1
f(n) = O(g(n))
예를 들겠습니다.
f(n) = 3n+2 and g(n) = n
f(n) = O(g(n))
f(n) <= C * g(n) , c > 0 , n0 >= 1
3n+2 <= c*n
take c = 4
3n+2 <= 4n => n >= 2
우리는 C*g(n) 를 선택할 수 있다. 왜냐하면 g(n) = n^2 or n^3 ... n^n 는 f(n) 에 쓸 수 있지만, 가장 작은 것을 취하는 것이 가장 좋다 g(n)Ω로 표시된 큰 Ω

f(n) >= C*g(n) ; n >= n0 ; c>0 , n0 >= 1
f(n) = O(g(n))
인스턴스
f(n) = 3n+2 and g(n) = n
f(n) = O(g(n))
f(n) >= C * g(n)
3n+2 >= c*n
take c = 1 and n0 >= 1
3n+2 = Ω(n)
예제 2
g(n) = 3n+2 g(n)=n^2
3n+2 ?= Ω(n^2)
3n+2 >= c*n^2 , n0
우리는 이 해답을 만족시킬 수 없습니다n. 따라서 C보다 낮은 것을 선택해야 합니다. 예를 들어 n 또는 log(n)Θ로 나타낸 대θ

f(n) = Θ(g(n))
c1*g(n) <= f(n) <= c2*gn(n) ; c1,c2 > 0 , n >= n0
인스턴스
f(n) = 3n+2 , g(n) = n
f(n) <= C2*g(n)
take c2 = 4
3n+2 <= 4n
f(n) >= c1*g(n)
take c1 = 1
3n+2 >= n , n0 >= 1
log(log(n)) 이것은 그들의 시간이 이보다 길지 않다는 것을 의미하며 이것은 최악의 상황이라고 불린다.O 이것은 그들의 시간이 이보다 더 좋지 않다는 것을 의미하며 이것은 가장 좋은 상황이라고 불린다.Ω 이것은 평균 사례라는 것을 의미하며 평균 사례라고 불린다.
우리는 통상적으로 가장 좋은 상황에 관심을 갖지 않는다. 우리는 가장 나쁜 상황에 관심을 갖는다.만약 최악과 가장 좋은 상황이 같다면, 우리는 통상적으로 평균 상황을 선택한다.
예: Θ 개의 요소를 포함하는 그룹을 예로 들다
0
일.
이.
삼.
사.
오.
육.
칠.
오.
칠.
일.
이.
사.
십
이십
십일
만약에 우리가 원소n를 찾아야 한다고 가정하면 가장 좋은 상황은 x, 가장 나쁜 상황은 Ω(1), 평균 상황은 O(n)시간 복잡도 분석
Θ(n/2)= Θ(n)는 실시간이 아니라 프로그램 완성에 필요한 근사 시간일 뿐이다.
두 가지 알고리즘이 있습니다.
iterative:
A()
{
for i=1 to n
max(a,b)
}
recursive:
A(n)
{
if() A(n/2)
}
어떤 교체도 차례로 쓸 수 있고, 반대로도 마찬가지다.
알고리즘이 순환하거나 귀속되지 않으면 시간 복잡도는 상수f(n), 시간 복잡도O(1)가 되면 최대 단계를 취하기 때문에 취O(n^2+n)예제
A()
{
int i;
for(i = 1 to n) pf("text");
}
time complexity : O(n)
A()
{
int i;
for(i = 1 to n)
for(j = 1 to n)
pf("omar");
}
time complexity : O(n^2)
A()
{
int i;
while (s <= n)
{
i++;
s = s+i;
pf("omar");
}
}
time complexity : O(sqrt(n))
/*
Analysing :
s : 1 3 6 10 15 21 ...
i : 1 2 3 4 5 6 ...
s will stop on n
let's say k is the final i
and s is nothing but new i + all old i (6 = 3+2+1) so it will stop when it reach
k(k+1)/2 > n
(k^2+k)/2 > n
k = O(sqrt(n))
*/
A()
{
int i;
for(i=1;i^2<=n;i++) pf("omar");
}
time complexity : O(sqrt(n))
// Here all the cases are the same
A()
{
int i,j,k,n;
for(i=1 ; i<n ; i++)
{
for(j=1;j<=i;j++)
{
for(k=1 ; k <= 100 ; k++)
{
pf("omar");
}
}
}
}
time complexity : O(n^2)
/*
Analysing :
i = 1 , j = 1 time , k = 100 times
i = 2 , j = 2 times , k = 200 times
i = 3 , j = 3 times , k = 300 times
...
i = n , j = n times , k = j*100 times
1*100+2*100+3*100+...+n*100
= 100 (1+2+3+...+n)
= 100 (n(n+1)/2) = O(n^2)
*/
int i,j,k,n;
for(i = 1 ; i <= n ;i++)
{
for(j=1 ; j <= i^2 ; j++)
{
for(k=1 ; k <= n/2 ; k++)
{
pf("omar");
}
}
}
time complexity : O(n^4)
/*
Analysing :
i = 1 , j = 1 time , k = n/2 * 1
i = 2 , j = 4 times , k = n/2 * 4
i = 3 , j = 9 times , k = n/2 * 9
...
i = n , j = n^2 times , k = n/2 * n^2 times
n/2 * 1 + n/2 *4 + n/2 * 9 + ... + n/2 * n^2
= n/2 * (n(n+1)(2n+1))/6
= O(n^4)
*/
A()
{
for(i = 1 ; i < n ; i = i*2)
pf("omar");
}
time complexity : O(log(n))
/*
Analysing :
i : 1 , 2 , 4 ... n
2^0 , 2^1 , 2^2 ... 2^k
2^k = n => k = log(n) = O(log(n))
since i is multiplied by 2 every step so log here is base 2
if i is multiplied by k we say log of base k
*/
A()
{
int i,j,k;
for(i=n/2 ; i <= n ; i++)
for(j=1 ; j <= n2 ; j++)
for(k=1 ; k <= n ; k=k*2)
pf("omar");
}
time complexity : O(n^2 * log(n))
/*
Analysing :
n/2 * n/2 * log(n) = O(n^2 * log(n))
*/
A()
{
int i,j,k;
for(i=n/2 ; i <= n ; i++) // n/2
for(j=1 ; j <= n ; i = 2*k) // log n
for(k=1 ; k <= n ; k = k*2) // log n
pf("omar");
}
time complexity : O(n*(log(n))^2)
A()
{
// assume n >= 2
while(n>1)
{
n = n/2;
}
}
time complexity : O(log(n))
A()
{
for(i = 1 ; i <= n ; i++) // n
for(j = 1 ; j <= n ; i = j+i) //
pf("omar")
}
time complexity : O(n*log(n))
/*
Analysing :
i = 1 , j = 1 to n ; n times
i = 2 , j = 1 to n ; n/2 times
i = 3 , j = 1 to n ; n/3 times
...
i = n , j = 1 to n ; n/n times
n(1+ 1/2 + 1/3 + ... + 1/n )
= n (log n) = O(n * log(n))
*/
A()
{
int n = (2^2)^k;
for(i=1;i<=n;i++) // n
{
j = 2
while(j <= n)
{
j = j^2;
pf("omar");
}
}
}
time complexity : O(log(log(n)))
/*
Analysing :
k = 1 ; n = 4 ; j = 2,4 ; n * 2 times
k = 2 ; n = 16 ; j = 2,4,16 ; n * 3 times
k = 3 ; n = (2^2)^3 ; j = 2^1,2^2,2^4,2^8 ; n * 4 times
n = (2^2)^k => log n = 2^k => log(log(n))=k
n*(k+1) = n(log(log(n)) + 1) = O(log(log(n)))
*/
귀속 알고리즘의 시간 분석
A(n)
{
if(...)
return A(n/2)+A(n/2);
}
T(n) = c+2*T(n/2)
A(n)
{
if(n>1) return A(n-1);
}
T(n) = 1 + T(n-1)
= 1 + 1 + T(n-2)
= 2+1+T(n-3)
= k+T(n-k) // k = n-1
= (n-1)+T(1) = n-1+1 = n
대칭 이동
T(n-1) = 1+T(n-2) -> 2
T(n-2) = 1+T(n-3) -> 3
T(n) = n + T(n)
T(n-1) = (n-1)+T(n-2)
T(n-2) = (n-2)+T(n-3)
-----------------------
T(n) = n + T(n-1)
= n + (n-1) + T(n-2)
= n + (n-1) + (n-2) + T(n-3)
= n + (n-1) + (n-2)+...+(n-k)+T(n-(k+1))
with n-(k+1)=1 => n-k-1=1 => k=n-2
= n+(n-1)+(n-2)+...+(n-(n-2))+T(n-(n-2+1))
= n+(n-1)+(n-2)+...+1
= n(n-1)/2
= O(n^2)
귀속 트리 방법
T(n) = 2*T(n/2) + C ; n>1
= C ; n = 1

T(1) = T(n/n)
c+2c+4c+...+nc
c(1+2+4+...+n)
c(1+2+4+...+2^k)
c(1 (2^(k+1) - 1) / (2-1) )
c(2^k+1 - 1)
c(2n-1)
O(n)
T(n) = 2*T(n/2)+n ; n > 1
= 1 ; n = 1

다양한 기능 비교
만약에 우리가 두 개의 함수O(n^2)와 n^2가 있다고 가정하면 그것들n^3은 똑같이 흔하기 때문에 나는 그것을 n^2과1로 다시 쓴다.n과f(n)를 제시하면, 우리는 가장 큰 것을 취하여 그것들을 비교한다.만약 그것들이 g(n)과 2 같은 상수라면, 우리는 그것들이 같다고 생각한다.
예제
2^n n^2
n log(2) 2 log(n)
n 2*log(n)
consider n = 2^100
2^100 2*log(2^100)
2^100 200
2^100 >>>>>>>>>>>>>>>>>>> 200
so 2^n growing very large
3^n 2^n
n*log(3) n*log(2)
cancel n and compare it
log(3) log(2)
n^2 n*log(n)
concel common terms
n*n n*log(n)
n > log(n)
n log(n)^100
log(n) 100*log(log(n))
take n = 2^128
128 100*log(128)
128 700
let's take n = 1024
1024 100*log(1024)
1024 1000
so n growing larger
n^log(n) n*log(n)
log(n)*log(n) log(n)+log(log(n))
for n = 10^1024
1024*1024 1034
for n = (2^2)^20
2^20*2^20 2^20+20
so n^log(n) is larger
sqrt(log(n)) log(log(n))
1/2 * log(log(n)) log(log(log(n)))
take n = (2^2)^10
5 3.5
n^(sqrt(n)) n^log(n)
sqrt(n)*log(n) log(n)*log(n)
sqrt(n) log(n)
1/2 * log(n) log(log(n))
n = 2^128
64 7
f(n) = {
n^3 0<n<10000
n^2 n>=10000
}
g(n) = {
n 0 < n < 100
n^3 n > 100
}
0-99
100-9999
10,000 ....
f(n)
n^3
n^3
n^2
g(n)
n
n^3
n^3
우리는 무한대 중의 함수에 관심을 가지기 때문에 4 무한대 중에서 더욱 크다
마스터스의 정리
우선g(n)과log^2(n) 사이가 다르다. 왜냐하면(log(n))^2과(log(n))^2 = log(n) * log(n)마스터스의 정리는 은일 문제를 해결하는 데 쓰인다
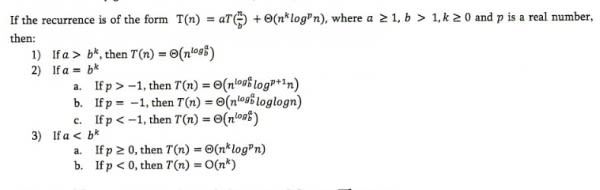
예제
T(n) = 3T(n/2) + n^2
a = 3 , b = 2 , k = 2 p=0
a < b^k
3 < 4
so it's the case 3)a so T(n) = O(n^2 * log^0(n))
T(n) = 4*T(n/2) + n^2
a=4 , b=2 , k=2 , p=0
4=2^2
so it's case 2)a T(n) = O(n^log(4) * log(n)) = O(n^2*log(n))
T(n) = T(n/2)+n^2
a=1 , b=2 , k=2 , p=0
1 < 2^2
it's case 3)a T(n) = O(n^2 * log^0(n)) = O(n^2)
T(n) = 2^n*T(n/2)+n^n master theoreme is not applied
T(n) = 16*T(n/4)+n
a = 16 b=4 k=1 p=0
16>4
so it's 1)
T(n) = 2*T(n/2)+n*log(n)
a=2 b=2 k=1 p=1
2=2 , p>-1 so it's 2)a
만약 그것이 정리처럼 보이지 않는다면, 우리는 그것을 재구성해야 한다
T(n) = 2*T(n/2)+n/log(n)
= 2T(n/2)+n*log^-1(n)
a=2 , b =2 , k=1 p=-1
s = 2^1 so it's case 2)b
T(n) = 2*T(n/4)+n^0.51
a=2 b=4 k=051 p=0
2 < 4^0.51
case 3)a
T(n) = 05*T(n/2)+1/n
a=0.5 not valid
T(n) = 6*T(n/3)+n^2*log(n)
a=6 b=3 k=2 p=1
6 < 3^2
so it's 3)a
T(n) = 64 T(n/8) - n^2 * log(n)
can not apply master theorem
T(n) = 7*T(n/3)+n^2
a=7 b=3 k=2 p=0
7 < 3^2
case 3)a
T(n) = 4*T(n/2)+log(n)
a=4 b=2 k=0 p=1
4 > 2^0
case 1
T(n) = sqrt(2)*T(n/2)+log(n)
a=sqrt(2) b=2 k=0 p=1
sqrt(2) > 2^0
case 1
T(n) = 2*T(n/2)+sqrt(n)
a=2 b=2 k=1/2 p=0
2>2^1/2
case 1
T(n) = 3*T(n/2)+n
a=3 b=2 k=1 p=0
3 > 2^1
case 1
T(n) = 3*T(n/3)+sqrt(n)
a=3 b=3 k=1/2 p=0
3>3^1/2
case 1
T(n) = 4*T(n/2)+C*n
a=4 b=2 k=1 p=0
4 > 2^1
case 3)b
T(n)=3*T(n/4)+(n*log(n))
a=3 b=4 k=1 p=1
3 < 4
case 3)a
공간 복잡성 분석
시간의 복잡도와 마찬가지로, 우리는 교체 프로그램과 귀속 프로그램의 공간 복잡도가 있다.때때로 우리는 공간을 위해 시간을 희생한다.
Algo(A,1,n)
{
int i;
for(i=1 to n) A[i] = 0;
}
이 공간의 복잡도는 고정적이다log^2(n) = log(log(n)). 왜냐하면 우리는 초기 입력을 고려하지 않기 때문이다.그래서 우리는 추가 공간을 계산한다. 예를 들어 O(1)Algo(A,1,n)
{
int i;
create B[n];
for(i=1 to n) B[i] = A[i];
}
필요한 공간량은 i 입니다. 왜냐하면 우리는 O(n) 요소가 포함되어 있기 때문입니다.시간의 복잡도와 마찬가지로, 우리는 상수를 계산하지 않는다. 다시 말하면, 우리는 더욱 높은 단계를 취한다.
Algo(A,1,n)
{
create B[n,n];
int i,j;
for(i=1 to n)
for(j=1 to n) B[i,j]=A[i]
}
공간 복잡도B[n]A(n)
{
if(n>=1)
{
A(n-1);
pf(n);
}
}
프로그램이 매우 작기 때문에, 우리는 트리 방법을 사용하여 취할 것이다 n

호출이 끝날 때마다 인쇄되기 때문에 O(n^2) 로 출력됩니다.
공간 복잡도는 창고의 수량, 즉 n=3, 그중1 2 3이 상수이기 때문에 우리는 그것을 O(kn)로 쓴다
시간 복잡도k는 우리가 주정리를 응용할 수 있는 형식이 아니기 때문에 우리는 반대환을 사용해야 한다
T(n) =T(n-1)+1
T(n-1)=T(n-2)+1
T(n-2)=T(n-3)+1
T(n) = T(T(n-2)+1)+1
= T(n-2) +2
= (T(n-3)+1) +2
= T(n-3)+3
= T(n-k)+k
= T(n-n)+n
= T(0)+n
= 1+n
= O(n)
따라서 시간과 공간의 복잡도는 O(n)A(n)
{
if(n>=1)
{
A(n-1);
pf(n);
A(n-1);
}
}
반복 호출 수:
A(3) = 15 = 2^(3+1) - 1
A(2) = 7 = 2^(2+1) - 1
A(1) = 3 = 2^(1+1) - 1
A(n) = (2^n) - 1
이것은 공간 복잡도가 아니다. 창고는 창고의 4개 단원T(n) = T(n-1)+1만 계산해야 하기 때문에 창고가 도착할 때O(n)마다 자동으로 비워지기 때문에 A(0),A(1),A(2),A(3), 그중A(0)은 창고의 한 단원이 차지하는 크기이기 때문에 공간 복잡도는 (n+1)*k에 불과하다.
이를 최적화하기 위해 동적 계획, 즉 계산된 값을 저장하여 다시 계산하지 않도록 할 수 있다.
A(n) -> T(n)
{
if(n>=1)
{
A(n-1); -> T(n-1)
pf(n); -> 1
A(n-1); -> T(n-1)
}
}
T(n) = 2*T(n-1)+1 ; n > 0
T(n-1) = 2*T(n-2)+1
T(n-2) = 2*T(n-3)+1
T(n) = 2(2T(n-2)+1)
= 4T(n-2)+2+1
= 4(2T(n-3)+1)+2+1
= 8T(n-3)+7
= 2^k * T(n-k) + 2^(k-1)+...+2^2+2+1
= 2^n * T(0)+2^n-1 + 2^n-2 + ... + 2^2 + 2 + 1
= 2^n + 2^n-1 + 2^n-2 + ... + 2^2 + 2 + 1
= O(2^n+1) = O(2^n)
시간의 복잡도는 매우 크다k. 우리가 말한 바와 같이 우리는 동적 기획으로 시간의 복잡도를 낮출 수 있다.
Reference
이 문제에 관하여(#010 DS&A- 시간과 공간 분석), 우리는 이곳에서 더 많은 자료를 발견하고 링크를 클릭하여 보았다
https://dev.to/elkhatibomar/010-ds-a-time-and-space-analysis-3gpa
텍스트를 자유롭게 공유하거나 복사할 수 있습니다.하지만 이 문서의 URL은 참조 URL로 남겨 두십시오.
 우수한 개발자 콘텐츠 발견에 전념
(Collection and Share based on the CC Protocol.)
우수한 개발자 콘텐츠 발견에 전념
(Collection and Share based on the CC Protocol.)
시간과 공간 분석
점근 분석 도론
컴퓨터 과학의 모든 문제를 해결하기 위해서 우리는 보통 프로그램을 작성하는데, 프로그램을 작성하기 전에 형식화된 설명, 즉 알고리즘으로 작성하는 것이 가장 좋다.
만약에 우리가 문제가 하나 있다고 가정하면
P 우리는 프로그램을 써야 한다. 우리는 c로 그것을 써야 한다. 프로그램을 쓰려면 먼저 알고리즘을 써야 한다. 가설P에는 다른 해와 다른 해s1,s2,s3,s4....와 다른 해time가 많은데 그의 과학은 memory라고 한다.알고리즘에 사용되는 기호는 다음과 같습니다.
점근 기호
Oh는

입력이 증가함에 따라 시간이 증가하면 최악의 경우 또는 상위 경계
Design and analysis of algorithm 를 충족합니다.f(n) <= C*g(n) ; n >= n0 ; c>0 , n0 >= 1
f(n) = O(g(n))
f(n) = 3n+2 and g(n) = n
f(n) = O(g(n))
f(n) <= C * g(n) , c > 0 , n0 >= 1
3n+2 <= c*n
take c = 4
3n+2 <= 4n => n >= 2
C*g(n) 를 선택할 수 있다. 왜냐하면 g(n) = n^2 or n^3 ... n^n 는 f(n) 에 쓸 수 있지만, 가장 작은 것을 취하는 것이 가장 좋다 g(n)Ω로 표시된 큰 Ω
f(n) >= C*g(n) ; n >= n0 ; c>0 , n0 >= 1
f(n) = O(g(n))
f(n) = 3n+2 and g(n) = n
f(n) = O(g(n))
f(n) >= C * g(n)
3n+2 >= c*n
take c = 1 and n0 >= 1
3n+2 = Ω(n)
g(n) = 3n+2 g(n)=n^2
3n+2 ?= Ω(n^2)
3n+2 >= c*n^2 , n0
n. 따라서 C보다 낮은 것을 선택해야 합니다. 예를 들어 n 또는 log(n)Θ로 나타낸 대θ
f(n) = Θ(g(n))
c1*g(n) <= f(n) <= c2*gn(n) ; c1,c2 > 0 , n >= n0
f(n) = 3n+2 , g(n) = n
f(n) <= C2*g(n)
take c2 = 4
3n+2 <= 4n
f(n) >= c1*g(n)
take c1 = 1
3n+2 >= n , n0 >= 1
log(log(n)) 이것은 그들의 시간이 이보다 길지 않다는 것을 의미하며 이것은 최악의 상황이라고 불린다.O 이것은 그들의 시간이 이보다 더 좋지 않다는 것을 의미하며 이것은 가장 좋은 상황이라고 불린다.Ω 이것은 평균 사례라는 것을 의미하며 평균 사례라고 불린다.우리는 통상적으로 가장 좋은 상황에 관심을 갖지 않는다. 우리는 가장 나쁜 상황에 관심을 갖는다.만약 최악과 가장 좋은 상황이 같다면, 우리는 통상적으로 평균 상황을 선택한다.
예:
Θ 개의 요소를 포함하는 그룹을 예로 들다0
일.
이.
삼.
사.
오.
육.
칠.
오.
칠.
일.
이.
사.
십
이십
십일
만약에 우리가 원소
n를 찾아야 한다고 가정하면 가장 좋은 상황은 x, 가장 나쁜 상황은 Ω(1), 평균 상황은 O(n)시간 복잡도 분석
Θ(n/2)= Θ(n)는 실시간이 아니라 프로그램 완성에 필요한 근사 시간일 뿐이다.두 가지 알고리즘이 있습니다.
iterative:
A()
{
for i=1 to n
max(a,b)
}
recursive:
A(n)
{
if() A(n/2)
}
알고리즘이 순환하거나 귀속되지 않으면 시간 복잡도는 상수
f(n), 시간 복잡도O(1)가 되면 최대 단계를 취하기 때문에 취O(n^2+n)예제A()
{
int i;
for(i = 1 to n) pf("text");
}
time complexity : O(n)
A()
{
int i;
for(i = 1 to n)
for(j = 1 to n)
pf("omar");
}
time complexity : O(n^2)
A()
{
int i;
while (s <= n)
{
i++;
s = s+i;
pf("omar");
}
}
time complexity : O(sqrt(n))
/*
Analysing :
s : 1 3 6 10 15 21 ...
i : 1 2 3 4 5 6 ...
s will stop on n
let's say k is the final i
and s is nothing but new i + all old i (6 = 3+2+1) so it will stop when it reach
k(k+1)/2 > n
(k^2+k)/2 > n
k = O(sqrt(n))
*/
A()
{
int i;
for(i=1;i^2<=n;i++) pf("omar");
}
time complexity : O(sqrt(n))
// Here all the cases are the same
A()
{
int i,j,k,n;
for(i=1 ; i<n ; i++)
{
for(j=1;j<=i;j++)
{
for(k=1 ; k <= 100 ; k++)
{
pf("omar");
}
}
}
}
time complexity : O(n^2)
/*
Analysing :
i = 1 , j = 1 time , k = 100 times
i = 2 , j = 2 times , k = 200 times
i = 3 , j = 3 times , k = 300 times
...
i = n , j = n times , k = j*100 times
1*100+2*100+3*100+...+n*100
= 100 (1+2+3+...+n)
= 100 (n(n+1)/2) = O(n^2)
*/
int i,j,k,n;
for(i = 1 ; i <= n ;i++)
{
for(j=1 ; j <= i^2 ; j++)
{
for(k=1 ; k <= n/2 ; k++)
{
pf("omar");
}
}
}
time complexity : O(n^4)
/*
Analysing :
i = 1 , j = 1 time , k = n/2 * 1
i = 2 , j = 4 times , k = n/2 * 4
i = 3 , j = 9 times , k = n/2 * 9
...
i = n , j = n^2 times , k = n/2 * n^2 times
n/2 * 1 + n/2 *4 + n/2 * 9 + ... + n/2 * n^2
= n/2 * (n(n+1)(2n+1))/6
= O(n^4)
*/
A()
{
for(i = 1 ; i < n ; i = i*2)
pf("omar");
}
time complexity : O(log(n))
/*
Analysing :
i : 1 , 2 , 4 ... n
2^0 , 2^1 , 2^2 ... 2^k
2^k = n => k = log(n) = O(log(n))
since i is multiplied by 2 every step so log here is base 2
if i is multiplied by k we say log of base k
*/
A()
{
int i,j,k;
for(i=n/2 ; i <= n ; i++)
for(j=1 ; j <= n2 ; j++)
for(k=1 ; k <= n ; k=k*2)
pf("omar");
}
time complexity : O(n^2 * log(n))
/*
Analysing :
n/2 * n/2 * log(n) = O(n^2 * log(n))
*/
A()
{
int i,j,k;
for(i=n/2 ; i <= n ; i++) // n/2
for(j=1 ; j <= n ; i = 2*k) // log n
for(k=1 ; k <= n ; k = k*2) // log n
pf("omar");
}
time complexity : O(n*(log(n))^2)
A()
{
// assume n >= 2
while(n>1)
{
n = n/2;
}
}
time complexity : O(log(n))
A()
{
for(i = 1 ; i <= n ; i++) // n
for(j = 1 ; j <= n ; i = j+i) //
pf("omar")
}
time complexity : O(n*log(n))
/*
Analysing :
i = 1 , j = 1 to n ; n times
i = 2 , j = 1 to n ; n/2 times
i = 3 , j = 1 to n ; n/3 times
...
i = n , j = 1 to n ; n/n times
n(1+ 1/2 + 1/3 + ... + 1/n )
= n (log n) = O(n * log(n))
*/
A()
{
int n = (2^2)^k;
for(i=1;i<=n;i++) // n
{
j = 2
while(j <= n)
{
j = j^2;
pf("omar");
}
}
}
time complexity : O(log(log(n)))
/*
Analysing :
k = 1 ; n = 4 ; j = 2,4 ; n * 2 times
k = 2 ; n = 16 ; j = 2,4,16 ; n * 3 times
k = 3 ; n = (2^2)^3 ; j = 2^1,2^2,2^4,2^8 ; n * 4 times
n = (2^2)^k => log n = 2^k => log(log(n))=k
n*(k+1) = n(log(log(n)) + 1) = O(log(log(n)))
*/
귀속 알고리즘의 시간 분석
A(n)
{
if(...)
return A(n/2)+A(n/2);
}
T(n) = c+2*T(n/2)
A(n)
{
if(n>1) return A(n-1);
}
T(n) = 1 + T(n-1)
= 1 + 1 + T(n-2)
= 2+1+T(n-3)
= k+T(n-k) // k = n-1
= (n-1)+T(1) = n-1+1 = n
T(n-1) = 1+T(n-2) -> 2
T(n-2) = 1+T(n-3) -> 3
T(n) = n + T(n)
T(n-1) = (n-1)+T(n-2)
T(n-2) = (n-2)+T(n-3)
-----------------------
T(n) = n + T(n-1)
= n + (n-1) + T(n-2)
= n + (n-1) + (n-2) + T(n-3)
= n + (n-1) + (n-2)+...+(n-k)+T(n-(k+1))
with n-(k+1)=1 => n-k-1=1 => k=n-2
= n+(n-1)+(n-2)+...+(n-(n-2))+T(n-(n-2+1))
= n+(n-1)+(n-2)+...+1
= n(n-1)/2
= O(n^2)
T(n) = 2*T(n/2) + C ; n>1
= C ; n = 1

T(1) = T(n/n)
c+2c+4c+...+nc
c(1+2+4+...+n)
c(1+2+4+...+2^k)
c(1 (2^(k+1) - 1) / (2-1) )
c(2^k+1 - 1)
c(2n-1)
O(n)
T(n) = 2*T(n/2)+n ; n > 1
= 1 ; n = 1

다양한 기능 비교
만약에 우리가 두 개의 함수
O(n^2)와 n^2가 있다고 가정하면 그것들n^3은 똑같이 흔하기 때문에 나는 그것을 n^2과1로 다시 쓴다.n과f(n)를 제시하면, 우리는 가장 큰 것을 취하여 그것들을 비교한다.만약 그것들이 g(n)과 2 같은 상수라면, 우리는 그것들이 같다고 생각한다.예제
2^n n^2
n log(2) 2 log(n)
n 2*log(n)
consider n = 2^100
2^100 2*log(2^100)
2^100 200
2^100 >>>>>>>>>>>>>>>>>>> 200
so 2^n growing very large
3^n 2^n
n*log(3) n*log(2)
cancel n and compare it
log(3) log(2)
n^2 n*log(n)
concel common terms
n*n n*log(n)
n > log(n)
n log(n)^100
log(n) 100*log(log(n))
take n = 2^128
128 100*log(128)
128 700
let's take n = 1024
1024 100*log(1024)
1024 1000
so n growing larger
n^log(n) n*log(n)
log(n)*log(n) log(n)+log(log(n))
for n = 10^1024
1024*1024 1034
for n = (2^2)^20
2^20*2^20 2^20+20
so n^log(n) is larger
sqrt(log(n)) log(log(n))
1/2 * log(log(n)) log(log(log(n)))
take n = (2^2)^10
5 3.5
n^(sqrt(n)) n^log(n)
sqrt(n)*log(n) log(n)*log(n)
sqrt(n) log(n)
1/2 * log(n) log(log(n))
n = 2^128
64 7
f(n) = {
n^3 0<n<10000
n^2 n>=10000
}
g(n) = {
n 0 < n < 100
n^3 n > 100
}
100-9999
10,000 ....
f(n)
n^3
n^3
n^2
g(n)
n
n^3
n^3
우리는 무한대 중의 함수에 관심을 가지기 때문에
4 무한대 중에서 더욱 크다마스터스의 정리
우선
g(n)과log^2(n) 사이가 다르다. 왜냐하면(log(n))^2과(log(n))^2 = log(n) * log(n)마스터스의 정리는 은일 문제를 해결하는 데 쓰인다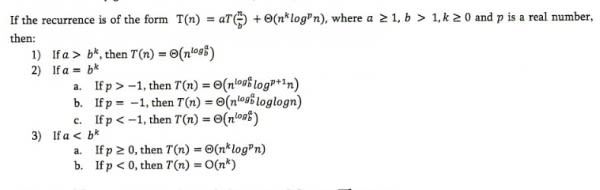
예제
T(n) = 3T(n/2) + n^2
a = 3 , b = 2 , k = 2 p=0
a < b^k
3 < 4
so it's the case 3)a so T(n) = O(n^2 * log^0(n))
T(n) = 4*T(n/2) + n^2
a=4 , b=2 , k=2 , p=0
4=2^2
so it's case 2)a T(n) = O(n^log(4) * log(n)) = O(n^2*log(n))
T(n) = T(n/2)+n^2
a=1 , b=2 , k=2 , p=0
1 < 2^2
it's case 3)a T(n) = O(n^2 * log^0(n)) = O(n^2)
T(n) = 2^n*T(n/2)+n^n master theoreme is not applied
T(n) = 16*T(n/4)+n
a = 16 b=4 k=1 p=0
16>4
so it's 1)
T(n) = 2*T(n/2)+n*log(n)
a=2 b=2 k=1 p=1
2=2 , p>-1 so it's 2)a
T(n) = 2*T(n/2)+n/log(n)
= 2T(n/2)+n*log^-1(n)
a=2 , b =2 , k=1 p=-1
s = 2^1 so it's case 2)b
T(n) = 2*T(n/4)+n^0.51
a=2 b=4 k=051 p=0
2 < 4^0.51
case 3)a
T(n) = 05*T(n/2)+1/n
a=0.5 not valid
T(n) = 6*T(n/3)+n^2*log(n)
a=6 b=3 k=2 p=1
6 < 3^2
so it's 3)a
T(n) = 64 T(n/8) - n^2 * log(n)
can not apply master theorem
T(n) = 7*T(n/3)+n^2
a=7 b=3 k=2 p=0
7 < 3^2
case 3)a
T(n) = 4*T(n/2)+log(n)
a=4 b=2 k=0 p=1
4 > 2^0
case 1
T(n) = sqrt(2)*T(n/2)+log(n)
a=sqrt(2) b=2 k=0 p=1
sqrt(2) > 2^0
case 1
T(n) = 2*T(n/2)+sqrt(n)
a=2 b=2 k=1/2 p=0
2>2^1/2
case 1
T(n) = 3*T(n/2)+n
a=3 b=2 k=1 p=0
3 > 2^1
case 1
T(n) = 3*T(n/3)+sqrt(n)
a=3 b=3 k=1/2 p=0
3>3^1/2
case 1
T(n) = 4*T(n/2)+C*n
a=4 b=2 k=1 p=0
4 > 2^1
case 3)b
T(n)=3*T(n/4)+(n*log(n))
a=3 b=4 k=1 p=1
3 < 4
case 3)a
공간 복잡성 분석
시간의 복잡도와 마찬가지로, 우리는 교체 프로그램과 귀속 프로그램의 공간 복잡도가 있다.때때로 우리는 공간을 위해 시간을 희생한다.
Algo(A,1,n)
{
int i;
for(i=1 to n) A[i] = 0;
}
log^2(n) = log(log(n)). 왜냐하면 우리는 초기 입력을 고려하지 않기 때문이다.그래서 우리는 추가 공간을 계산한다. 예를 들어 O(1)Algo(A,1,n)
{
int i;
create B[n];
for(i=1 to n) B[i] = A[i];
}
i 입니다. 왜냐하면 우리는 O(n) 요소가 포함되어 있기 때문입니다.시간의 복잡도와 마찬가지로, 우리는 상수를 계산하지 않는다. 다시 말하면, 우리는 더욱 높은 단계를 취한다.Algo(A,1,n)
{
create B[n,n];
int i,j;
for(i=1 to n)
for(j=1 to n) B[i,j]=A[i]
}
B[n]A(n)
{
if(n>=1)
{
A(n-1);
pf(n);
}
}
n

호출이 끝날 때마다 인쇄되기 때문에
O(n^2) 로 출력됩니다.공간 복잡도는 창고의 수량, 즉
n=3, 그중1 2 3이 상수이기 때문에 우리는 그것을 O(kn)로 쓴다시간 복잡도
k는 우리가 주정리를 응용할 수 있는 형식이 아니기 때문에 우리는 반대환을 사용해야 한다T(n) =T(n-1)+1
T(n-1)=T(n-2)+1
T(n-2)=T(n-3)+1
T(n) = T(T(n-2)+1)+1
= T(n-2) +2
= (T(n-3)+1) +2
= T(n-3)+3
= T(n-k)+k
= T(n-n)+n
= T(0)+n
= 1+n
= O(n)
O(n)A(n)
{
if(n>=1)
{
A(n-1);
pf(n);
A(n-1);
}
}
A(3) = 15 = 2^(3+1) - 1
A(2) = 7 = 2^(2+1) - 1
A(1) = 3 = 2^(1+1) - 1
A(n) = (2^n) - 1
T(n) = T(n-1)+1만 계산해야 하기 때문에 창고가 도착할 때O(n)마다 자동으로 비워지기 때문에 A(0),A(1),A(2),A(3), 그중A(0)은 창고의 한 단원이 차지하는 크기이기 때문에 공간 복잡도는 (n+1)*k에 불과하다.이를 최적화하기 위해 동적 계획, 즉 계산된 값을 저장하여 다시 계산하지 않도록 할 수 있다.
A(n) -> T(n)
{
if(n>=1)
{
A(n-1); -> T(n-1)
pf(n); -> 1
A(n-1); -> T(n-1)
}
}
T(n) = 2*T(n-1)+1 ; n > 0
T(n-1) = 2*T(n-2)+1
T(n-2) = 2*T(n-3)+1
T(n) = 2(2T(n-2)+1)
= 4T(n-2)+2+1
= 4(2T(n-3)+1)+2+1
= 8T(n-3)+7
= 2^k * T(n-k) + 2^(k-1)+...+2^2+2+1
= 2^n * T(0)+2^n-1 + 2^n-2 + ... + 2^2 + 2 + 1
= 2^n + 2^n-1 + 2^n-2 + ... + 2^2 + 2 + 1
= O(2^n+1) = O(2^n)
k. 우리가 말한 바와 같이 우리는 동적 기획으로 시간의 복잡도를 낮출 수 있다.
Reference
이 문제에 관하여(#010 DS&A- 시간과 공간 분석), 우리는 이곳에서 더 많은 자료를 발견하고 링크를 클릭하여 보았다 https://dev.to/elkhatibomar/010-ds-a-time-and-space-analysis-3gpa텍스트를 자유롭게 공유하거나 복사할 수 있습니다.하지만 이 문서의 URL은 참조 URL로 남겨 두십시오.

좋은 웹페이지 즐겨찾기
