Numpy (5)
🥴 Numpy (5)
📌 Matrix
데이터 분석에 있어서 Matrix를 빼놓고 이야기 할 수가 없다.
📌 덧셈
- 덧셈을 하는 경우에는 shape가 동일해야 된다. 그리고 shape는 계속 유지된다.
- a + b
- np.sum(a, b, axis = 축 적어주기)
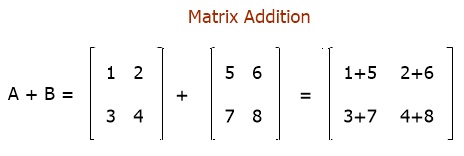
a = np.array([[1, 2, 3],
[2, 3, 4]])
np.sum(a, axis = 0) # 위에서 아래로 더하기
np.sum(a, axis = 1) # 왼쪽에서 오른쪽으로 더하기
📌 뺄셈
- 뺄셈을 하는 경우에는 shape가 동일해야 된다. 그리고 shape는 계속 유지된다.
- a - b
📌 곱셈 (Dot Product)
- 곱셈 ≠ Dot product
곱셈인 경우에는, 위와 같이 shape가 동일하면 된다.
같은 포지션에 있는 경우 > 일반 곱셈을 이용하면 된다.
일반적인 곱셈인 a * b 이용하기.
- np.dot(a, b)
a = np.array([[1, 2, 3],
[2, 3, 4]])
b = np.array([[3, 4, 5],
[1, 2, 3]])
a * b
- Dot product인 경우, 맞닿는 shape가 동일해야 된다.

a = np.array([[3, 4, 5],
[1, 2, 3],
[7, 8, 9]])
b = np.array([[1, 2],
[3, 4],
[5, 6]])
np.dot(a,b)
📌 Broadcasting
a = np.array([[1, 2, 3],
[2, 3, 4]])
a+3
a-3
a*3
a/3
이처럼 알아서 shape를 맞춰주기 때문에 굳이 ndarray 형태를 만들어줘서 사칙연산을 할 필요가 전혀 없다~!
😀 마무리...
데이터 분석에 있어서 Matrix를 빼놓고 이야기 할 수가 없다.
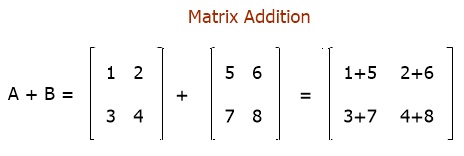
a = np.array([[1, 2, 3],
[2, 3, 4]])
np.sum(a, axis = 0) # 위에서 아래로 더하기
np.sum(a, axis = 1) # 왼쪽에서 오른쪽으로 더하기곱셈인 경우에는, 위와 같이 shape가 동일하면 된다.
같은 포지션에 있는 경우 > 일반 곱셈을 이용하면 된다.
일반적인 곱셈인 a * b 이용하기.
a = np.array([[1, 2, 3],
[2, 3, 4]])
b = np.array([[3, 4, 5],
[1, 2, 3]])
a * b
a = np.array([[3, 4, 5],
[1, 2, 3],
[7, 8, 9]])
b = np.array([[1, 2],
[3, 4],
[5, 6]])
np.dot(a,b) a = np.array([[1, 2, 3],
[2, 3, 4]])
a+3
a-3
a*3
a/3이처럼 알아서 shape를 맞춰주기 때문에 굳이 ndarray 형태를 만들어줘서 사칙연산을 할 필요가 전혀 없다~!
데이터 분석에서는 Matrix가 중요하기 때문에, 연산은 어떻게 하는건지 Broadcasting을 잘 이해하고 사용할 수 있는지가 중요하다~!
- np.sum(a, b, axis = 축) > 축을 기준으로 연산 ≠ a + b > 같은 포지션에 있는 경우에 연산
- np.dot(a, b) > dot product ≠ a * b > 같은 포지션에 있는 경우에 연산
좌우가 같지 않음을 꼭 기억해두기. 각자 필요한 곳이 다 따로 있다.
Author And Source
이 문제에 관하여(Numpy (5)), 우리는 이곳에서 더 많은 자료를 발견하고 링크를 클릭하여 보았다 https://velog.io/@tino-kim/Numpy-5저자 귀속: 원작자 정보가 원작자 URL에 포함되어 있으며 저작권은 원작자 소유입니다.

좋은 웹페이지 즐겨찾기
